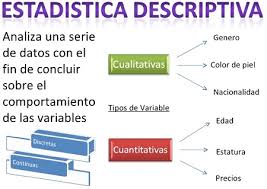
La estadística es la parte de las Matemáticas que estudia cómo recopilar y resumir gran cantidad de información para extraer conclusiones.
Existen
dos tipos de estadística:
·
Estadística
descriptiva
·
Estadística
inferencial
Estadística descriptiva:
Se
centra en recoger datos aleatoriamente,
para posteriormente clasificarlos,
representarlos gráficamente y
convertir dicha información en
estadísticos, que permitirán obtener conclusiones sin hacer generalizaciones o
predicciones a partir de ellos.
Estadística
inductiva o inferencial:
Maneja
el concepto de probabilidad basado en estudios previos de la estadística
descriptiva, que le permite establecer conclusiones o predicciones sobre una
población ante situaciones específicas.
La población de un estudio estadístico es el conjunto de elementos objeto de estudio.
Cada elemento se denomina individuo.
Cuando el número de individuos de la población es muy grande, tomamos una parte de ésta, denominada muestra.
La muestra es un subconjunto de la población y tiene que ser representativa de la misma.
La variable estadística es la propiedad o característica de la población que estamos interesados en estudiar. Puede ser cualitativa o cuantitativa.
.- Las variables cualitativas toman valores no numéricos.
.- Las variables cuantitativas toman valores numéricos. Entre ellas, distinguimos dos tipos: discretas y continuas.
- Las variables cuantitativas discretas no pueden tomar valores intermedios entre dos valores posibles consecutivos.
- Las variables cuantitativas continuas pueden tomar valores intermedios entre dos valores tan próximos como deseemos.
Ejemplo 1
Se
desea realizar un estudio estadístico
con algunas personas de algún municipio acerca de la necesidad o no
del pico y placa para los
automóviles.
- La Población: es el conjunto de estudio más grande, para este caso las personas del municipio.
- La Muestra: es el subconjunto de estudio más pequeño que la población, para este caso algunas personas del municipio (personas con las que se realizó la encuesta).
- La Variables es la necesidad o no del pico y placa para los automóviles, la cual vendría hacer una Variable Cualitativa.
Ejemplo 2
En la entrada de un concierto se pregunta a un grupo de espectadores desde que población se desplazaron
para asistir al concierto.
- La Población: es el conjunto de estudio más grande, para este caso las personas que asistieron al concierto..
- La Muestra: es el subconjunto de estudio más pequeño que la población, para este caso grupo de espectadores que fueron encuestados.
- La Variables es la población desde donde se desplazaron para asistir al concierto, la cual vendría hacer una Variable Cualitativa.
Gráficos estadísticos
Un estudio o investigación, que incluya recabar datos acerca de diversos tipos de variables estadísticas, se ve enriquecido con la elaboración de distintos tipos de gráficas estadísticas.
El gran mérito de estos instrumentos, es
que los datos se transforman casi instantáneamente en información, y
pueden ser -en general- analizados casi de forma intuitiva.
Un detalle importante a señalar es que
existen varios tipos de gráficas estadísticas y que cada una de será
adecuada para diferentes tipos de estudios. En otras palabras, hay
estudios donde se busca comparar, otros buscan detectar mayorías o minorías, otros quieren determinar tendencias, otros incidencias, etc.
En todos los casos, uno en especial será el gráfico más adecuado y claro. Los gráficos estadísticos más usuales son:
- Gráfico o diagrama de barras
- Gráfico o diagrama de sectores
- Histograma
- Polígono de frecuencias
- Pictograma
Ejemplos de gráficos estadísticos
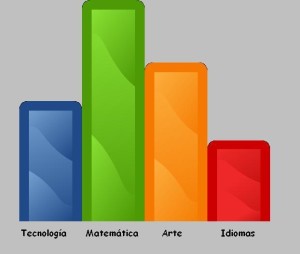
- Gráfico o diagrama de barras
Un gráfico de barras,
suele expresar mediante la elevación de barras de diferente color
(pueden ser horizontales) aquella información que intenta dilucidar un
sólo aspecto entre un grupo de personas encuestadas. Depende de cómo
haya sido graduado el eje vertical “y”, se expresará en distintas
unidades o valores el impacto de los resultados en cuestión. Puede
usarse para representar porcentajes, pero en esta circunstancia suele
ser otro el tipo de gráfico elegido. He aquí un ejemplo de este tipo de
gráficos, que emula ser las respuestas entre un grupo de estudiantes
acerca de cuál es la materia que más disfruta estudiar en la escuela:
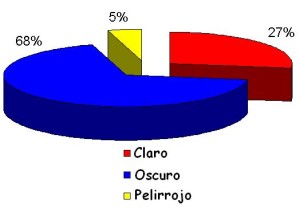
- Gráfico o diagrama de Sectores
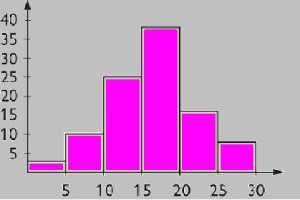
- Histograma
Se trata de una representación gráfica
de una variable determinada a través de barras, en las cuales su
superficie es proporcional a la frecuencia de los
valores hallados. El eje vertical marca las frecuencias, y el
horizontal los valores posibles de las variables. He aquí un ejemplo:
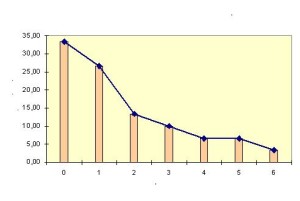
- Polígono de frecuencias
Se trata de un tipo de gráfico lineal
que utilizamos para la representación de la incidencia de respuesta de
una variable cuantitativa. El polígono surge de unir los puntos medios
de las bases superiores de las barras de un diagrama de barras, e
incluso también de un histograma.He aquí un ejemplo de este tipo de
gráficos estadísticos.
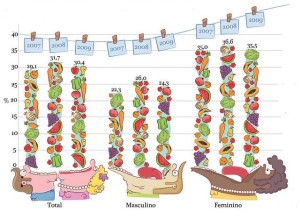
- Pictograma
Se trata de un gráfico donde se sustituyen los elementos abstractos (como las barras) por dibujos relativos a la temática
de lo que se está graficando. Eso sí: su tamaño debe ser proporcional a
la frecuencia que representen; para una mayor claridad se sugiere
indicarla. La imagen es elocuente: trata sobre los resultados de una
encuesta tratando de saber cuántas veces por semana comen las personas
frutas o verduras.
Fuente: http://matematicasmodernas.com/tipos-de-graficas-estadisticas/TIPOS DE GRÁFICOS
CLASES DE GRAFICAS ESTADISTICAS de guestb0c835
MODA
La moda es el valor que aparece con mayor frecuencia dentro de una muestra.
 es el símbolo de la media aritmética.
es el símbolo de la media aritmética.

La tabla de frecuencias es una herramienta que permite ordenar los datos de manera que se presentan numéricamente las características de la distribución de un conjunto de datos o muestra.
La suma de las frecuencias absolutas de todos los elementos diferentes del conjunto debe ser el número total de sujetos N. Si el conjunto tiene k números (o categorías) diferentes, entonces:



Las frecuencias relativas son valores entre 0 y 1, 0 ≤ fi ≤ 1. La suma de las frecuencias relativas de todos los sujetos da 1. Supongamos que en el conjunto tenemos k números (o categorías) diferentes, entonces:

Si se multiplica la frecuencia relativa por cien se obtiene el porcentaje (tanto por cien %).

La frecuencia relativa acumulada de cada valor siempre es mayor que la frecuencia relativa. De hecho, la frecuencia relativa acumulada de un elemento es la suma de las frecuencias relativas de los elementos menores o iguales a él, es decir:

Más información
MODA
La moda es el valor que aparece con mayor frecuencia dentro de una muestra.
Se representa por Mo.
Se puede hallar la moda para variables cualitativas y cuantitativas.
Hallar la moda de la distribución:
2, 3, 3, 4, 4, 4, 5, 5 Mo= 4
Si en un grupo hay dos o varias puntuaciones con la misma frecuencia y esa frecuencia es la máxima, la distribución es bimodal o multimodal, es decir, tiene varias modas.
1, 1, 1, 4, 4, 5, 5, 5, 7, 8, 9, 9, 9Mo= 1, 5, 9
Cuando todas las puntuaciones de un grupo tienen la misma frecuencia, no hay moda.
2, 2, 3, 3, 6, 6, 9, 9
Si dos puntuaciones adyacentes tienen la frecuencia máxima, la moda es el promedio de las dos puntuaciones adyacentes.
0, 1, 3, 3, 5, 5, 7, 8Mo = 4
Mediana
Es el valor que ocupa el lugar central de todos los datos cuando éstos están ordenados de menor a mayor.
La mediana se representa por Me.
La mediana se puede hallar sólo para variables cuantitativas.
Cálculo de la mediana
1 Ordenamos los datos de menor a mayor.
2 Si la serie tiene un número impar de medidas la mediana es la puntuación central de la misma.
2, 3, 4, 4, 5, 5, 5, 6, 6Me= 5
3 Si la serie tiene un número par de puntuaciones la mediana es la media entre las dos puntuaciones centrales.
7, 8, 9, 10, 11, 12Me= 9.5
Media aritmética
La media aritmética es el valor obtenido al sumar todos los datos y dividir el resultado entre el número total de datos.
 es el símbolo de la media aritmética.
es el símbolo de la media aritmética.
Tabla de frecuencias
La tabla de frecuencias (o distribución de frecuencias) es una tabla que muestra la distribución de los datos mediante sus frecuencias. Se utiliza para variables cuantitativas o cualitativas ordinales.La tabla de frecuencias es una herramienta que permite ordenar los datos de manera que se presentan numéricamente las características de la distribución de un conjunto de datos o muestra.
Frecuencia absoluta
La frecuencia absoluta (ni) de un valor Xi es el número de veces que el valor está en el conjunto (X1, X2,…, XN).La suma de las frecuencias absolutas de todos los elementos diferentes del conjunto debe ser el número total de sujetos N. Si el conjunto tiene k números (o categorías) diferentes, entonces:

Frecuencia absoluta acumulada
La frecuencia absoluta acumulada(Ni) de un valor Xi del conjunto (X1, X2,…, XN) es la suma de las frecuencias absolutas de los valores menores o iguales a Xi, es decir:Frecuencia relativa
La frecuencia relativa (fi) de un valor Xi es la proporción de valores iguales a Xi en el conjunto de datos (X1, X2,…, XN). Es decir, la frecuencia relativa es la frecuencia absoluta dividida por el número total de elementos N:

Frecuencia relativa acumulada
Definimos la frecuencia relativa acumulada (Fi) de un valor Xi como la proporción de valores iguales o menores a Xi en el conjunto de datos (X1, X2,…, XN). Es decir, la frecuencia relativa acumulada es la frecuencia absoluta acumulada dividida por el número total de sujetos N:
Más información
PARAMETROS DE DISPERSIÓN
Parámetros de dispersión. Son datos que informan de la concentración o
dispersión de los datos respecto de los parámetros de centralización.
Por ejemplo, vamos a suponer que hemos realizado el mismo examen en dos grupos
distintos. En uno, todos los alumnos han sacado la misma nota, un 5; en otro, la
mitad de los alumnos ha sacado un 0 y la otra mitad un 10. ¿Cuál es la media
en los dos casos? ¿Se pueden considerar los dos grupos iguales si la media
coincide?
Parece entonces que no es suficiente con las medidas de centralización, hace
falta otros parámetros que informen sobre la mayor o menor concentración de
los datos.

 Ejemplo:
Ejemplo:






Las medidas de dispersión son:
Rango o recorrido
El rango es la diferencia entre el mayor y el menor de los datos de una distribución estadística.
Desviación media
La desviación media es la media aritmética de los valores absolutos de las desviaciones respecto a la media.
La desviación media se representa por 



Calcular la desviación media de la distribución:
9, 3, 8, 8, 9, 8, 9, 18


Varianza
La varianza es la media aritmética del cuadrado de las desviaciones respecto a la media.
La varianza se representa por  .
.
 .
.

Ejercicios de varianza
Ejercicio 1:


Calcular la varianza de la distribución:
9, 3, 8, 8, 9, 8, 9, 18


Ejercicio 2:


Calcular la varianza de la distribución de la tabla:
| xi | fi | xi · fi | xi2 · fi | |
|---|---|---|---|---|
| [10, 20) | 15 | 1 | 15 | 225 |
| [20, 30) | 25 | 8 | 200 | 5000 |
| [30,40) | 35 | 10 | 350 | 12 250 |
| [40, 50) | 45 | 9 | 405 | 18 225 |
| [50, 60 | 55 | 8 | 440 | 24 200 |
| [60,70) | 65 | 4 | 260 | 16 900 |
| [70, 80) | 75 | 2 | 150 | 11 250 |
| 42 | 1 820 | 88 050 |


Desviación típica
La desviación típica es la raíz cuadrada de la varianza.
La desviación típica se representa por σ.


Ejercicios de desviación típica
Ejercicio 1:


Ejercicio 2:
Calcular la desviación típica de la distribución:
9, 3, 8, 8, 9, 8, 9, 18


Calcular la desviación típica de la distribución de la tabla:
| xi | fi | xi · fi | xi2 · fi | |
|---|---|---|---|---|
| [10, 20) | 15 | 1 | 15 | 225 |
| [20, 30) | 25 | 8 | 200 | 5000 |
| [30,40) | 35 | 10 | 350 | 12 250 |
| [40, 50) | 45 | 9 | 405 | 18 225 |
| [50, 60) | 55 | 8 | 440 | 24 200 |
| [60,70) | 65 | 4 | 260 | 16 900 |
| [70, 80) | 75 | 2 | 150 | 11 250 |
| 42 | 1 820 | 88 050 |


No hay comentarios:
Publicar un comentario